Cuantificación, el concepto

Cuantificar, la aproximación que permite la optimización:

Cuantificar parece una palabra de alguna acción compleja, pero realmente el concepto es bastante sencillo de entender. La cuantificación (o quantization) es el proceso por el cual se aproxima valores continuos a un conjunto de valores discretos o niveles, este proceso se puede realizar de forma uniforme o no uniforme, y se puede utilizar para reducir la precisión de los datos.

Vamos a aprender el concepto de una forma más sencilla y simple con un ejemplo:

1. Imaginemos que estas viendo la televisión, y esa televisión te permite modificar el volumen de una forma muy precisa, con sus decimales… te permite seleccionar un nivel de volumen dentro de unos valores «continuos».
   Pero existe otra empresa que ha decidido presentar su funcionalidad de volumen mucho más simple eliminando la flexibilidad, han creado 5 valores de volumen (silencio, bajo, medio, alto, máximo). Han cuantificado el volumen para mostrar 5 niveles diferentes, estos niveles son discretos porque no puedes elegir un nivel intermedio entre 2 valores.
   
   
2. Ahora imaginemos un intervalo que va de -1 a 1, donde una variable, llamémosla X puede ir desde -1 a 1, pudiendo optar cualquier valor, como por ejemplo X = -1, X = -0.8, X = 0.257… cualquier valor que nos imaginemos, pero solo dentro del intervalo. Imaginemos que queremos cuantificar ese intervalo para que X solo pueda optar uno de los 5 niveles,
   {-1, 0.5, 0, 0.5, 1}, y vamos a cuantificar los valores que puede tener X a esos 5 niveles.
   Imaginemos que tenemos muchas X guardadas, muchos valores… Una X que tenemos guardado podría ser X = 0.6, lo que vamos a hacer es asignar a esa X el nivel que esté más próximo a ese valor, en este caso 0.5 es el nivel más próximo a 0.6, por lo que esa X la guardamos como 0.5.
   Si nos fijamos bien, lo que estamos haciendo es aproximar esos valores a unos niveles que nosotros estamos definiendo, perdiendo precisión, ya que estamos guardando la información de forma aproximada, y el error máximo que podemos obtener en este caso es 0.25, pero si no necesitamos de tanta precisión acabamos de optimizar la información, ya que ahora tenemos 5 valores discretos y no infinitos que es como lo tendríamos si guardásemos la información de forma continua.
   
   
3. Veamos un ejemplo en el gif para entender que realiza de forma gráfica. Imaginemos que la función azul es la función que queremos cuantificar, y lo haremos con 6 niveles, del 0 al 5, es decir que cada punto de nuestra señal solo podrá tomar un valor entero (sin decimales) del 0 al 5, o dicho de otra forma intentar aproximar ese valor. Y nuestra función resultante es la función naranja.

Aplicaciones de la cuantificación

Como se puede ver en el ejemplo, gracias a la cuantificación podemos «decidir» la cantidad de niveles o valores puede tener un intervalo de muchísimos más valores. A simple vista se puede notar que nos sirve para simplificar la cantidad de valores que puede tomar un intervalo.

Realmente esto se aplica cada día en cada aplicación que requiera la tecnología, ya que los dispositivos electrónicos digitales, como ordenadores, móviles, que tengan microcontroladores como microondas, lavadoras… Aunque no se aplica de forma directa en todos. Cualquier componente digital necesita trabajar con datos, y esos datos se guardan en bits (0 o 1), eso significa que la precisión que podemos tener sobre un valor es limitado, ya que un valor puede tener una precisión de 8 bits, 16 bits… Eso quiere decir que no podemos tener infinitos decimales, no podemos cargar pi de forma completa en memoria, pero sí una aproximación muy buena, tanto que los decimales más pequeños dejan de tener relevancia práctica.

Sin embargo, podemos seguir optimizando la cantidad de información. Un sistema digital necesita «digitalizar» valores analógicos (valores continuos), como la señal que recibe una antena o las ondas que captura un micrófono, para poder operar con esos valores.
Pero quizá hay momentos donde queremos optimizar más la cantidad de niveles para que ocupe menos tamaño.

Imagina que quieres guardar un numero, X = 0.5006568, lo puedes hacer, pero es más fácil acordarte de X = 0.5 o X = 0.501 si necesitas más precisión. Con los ordenadores pasa algo parecido, ya que ese valor aproximado ocupa menos espacio, ¿y si no vas a utilizar toda esa precisión para que acordarte? Igual con el número pi, con 3.14 ya puedes hacer y calcular áreas y perímetros, con 3.141592 aún mejor pero quizá no sea necesario acordarse de tantos decimales si no lo requerimos, no obstante tampoco nos podemos pasar, no podemos decir que pi = 3 y suponer que vamos a realizar buenos cálculos con ello.

Adicionalmente, la cuantización también se aplica de forma similar para reducir la precisión de los parámetros de modelos de Inteligencia Artificial y Deep Learning, haciendo que los modelos sean más livianos y puedan procesarse con menos recursos computacionales, haciendo que puedan ejecutarse en hardware (la parte física de los dispositivos) menos costoso.

Ahora ya sabemos que es necesario para pasar de valores analógicos a digitales, y que es bueno para poder optimizar datos perdiendo precisión, pues la cuantificación es útil para algunos algoritmos de compresión como el jpeg, mp3… aunque el algoritmo de cuantificación no es tan sencillo, nosotros estamos aprendiendo el concepto de cuantificación y entenderemos la cuantificación uniforme, es decir que cada nivel esta separado y repartido de forma uniforme en todo el intervalo.

Ejemplo de cuantificación en audio

Vamos a empezar cuantificando un audio, primero veamos como suena este audio:

Este audio es un fragmento de Sinfonía núm. 40 de Mozart.

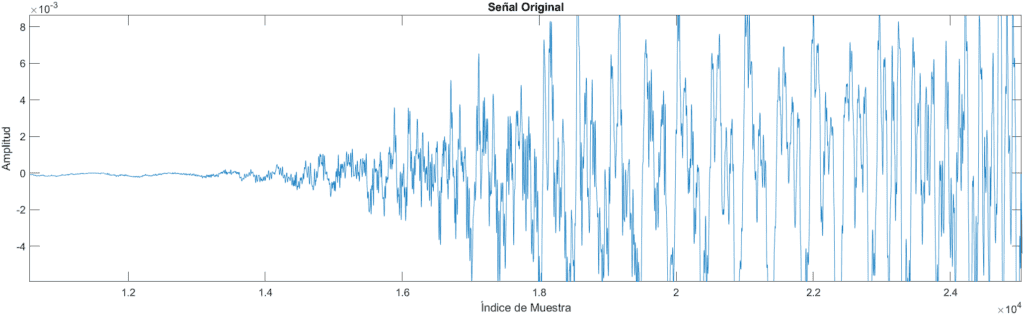
El audio actualmente tiene una precisión de 16 bits (realmente la precisión esta toqueteada por el algoritmo mp3, pero podemos considerar la resolución de bits del ejemplo práctico), cosa que hace que suene muy bien, ya que cada segundo captura 40 000 valores, y cada valor puede representar una posición de las 2^16 valores, lo que significa que cada punto puede tomar el valor de 0 a 65535, dentro de un intervalo de -1 a 1 (siendo 1 o -1 los valores más fuertes).

En esta gráfica podemos ver un pequeño fragmento del audio.

Cuantificación a 12 bits

Ahora cuantifiquemos el audio, utilizaremos la cuantificación más básica, la cuantificación uniforme para bajar esa precisión a valores de 12 bits, lo que hará que cada punto tenga hasta 2^12 valores, o lo que es lo mismo 4096 valores.
Guau parece un cambio radical, veamos como queda la señal de audio

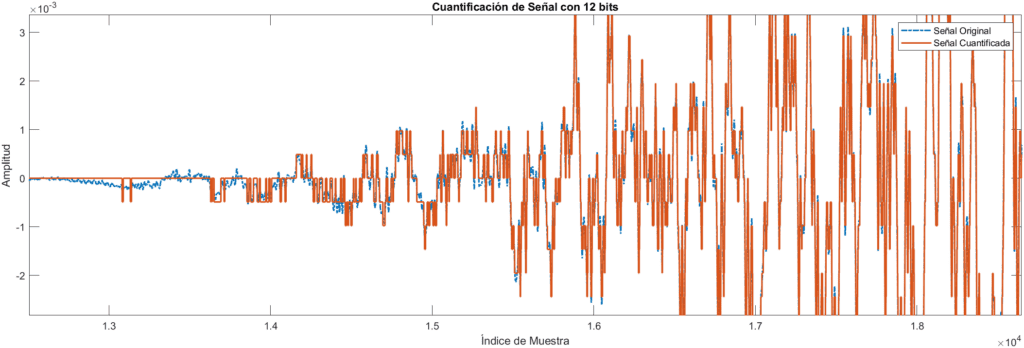
Podemos ver en la gráfica la función azul que es el audio original, y la naranja que es la señal cuantificada a 12 bits, podemos observar esos saltos que hace, como ya hemos mencionado antes, nos olvidamos de los valores «continuos» para asignarle un valor aproximado, eliminando la posibilidad de guardarlo como valores intermedios, lo que hace que la información pese menos y sea más fácil de trabajar.
Escuchemos el audio

Quizá podamos notar un pequeño cambio, pero realmente deberíamos compararlo uno detrás de otro para darnos cuenta.

Cuantificación a 8 bits

Cuantifiquemos a 8 bits, vamos a ver si notamos algo más la diferencia.
Ahora los valores que puede tomar cada punto son 2^8, lo que da 256 valores diferentes, como podemos observar se ha reducido mucho la capacidad y precisión que puede guardar nuestro archivo de audio, pero hemos optimizado mucho la cantidad de información necesaria para reproducir este audio.
Veamos la gráfica

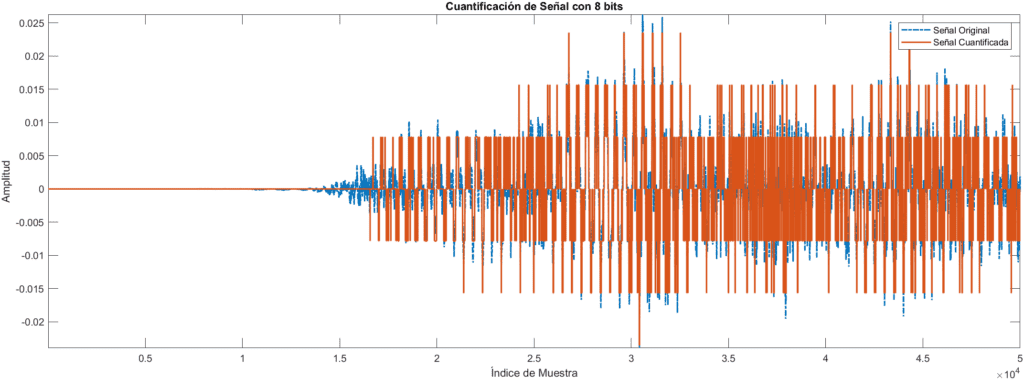
Ahora se nota mucho más que estamos perdiendo mucha información por el camino debido a esta aproximación

Con este audio ya estamos notando un desgaste demasiado grande, hemos rasgado la calidad del audio de forma considerable, también empezamos a escuchar el sonido que genera el error que estamos generando debido al procedimiento.

Cuantificación a 6 bits

Para ver como afectaría a este fragmento musical la caída a una precisión de 6 bits (2^6 = 64 valores), cuantifiquemos este audio una última vez a 6 bits.

Increíblemente sigue siendo reconocible, y se puede identificar la melodía, no obstante la calidad actual es pésima, si intentas vender esto a grupos musicales como un programa de optimización increíble no creo que llegues muy lejos.

¿Qué hacen otros algoritmos?

Existen métodos para mejorar ese error y poder comprimir esa información perdiendo otras partes que no sean tan importantes, y aquí entramos a la cuantificación no uniforme, algoritmos que intentan realizar lo mismo, aproximar la información, pero dejando más precisión para ciertas zonas más importantes.
Lamentablemente ese tema ya es más complejo y el objetivo de este artículo es enseñar el concepto de cuantificación de forma fácil, por lo que nos basta con entender la cuantificación uniforme.

Eso sí, para conseguir un algoritmo tan bueno para comprimir audio como el mp3 no solo basta con cuantificar, ellos utilizan una serie de métodos sofisticados, eliminando frecuencias que las personas no podemos oír, cuantificado dependiendo de la frecuencia, eliminando frecuencias enmascaradas por otras…
Todas esas técnicas hacen que puedan comprimir y quedarse con el 10%, 30%, 5%… del sonido original, y en muchas ocasiones siendo imperceptible incluso para oídos entrenados.

Ejemplo de cuantificación en imagen

Para ver ejemplos de cuantificación en imágenes, vamos a utilizar imágenes en escala de grises y probar a cuantificar el valor de la luminosidad de la imagen, así no lidiaremos con píxeles con múltiples valores como podríamos tener con color.

Como podemos observar la imagen está en escala de grises, donde cada pixel puede tener un valor de 0 a 255, es decir 8 bits de resolución, si aplicamos una cuantificación podremos observar en ciertas regiones de la imagen cambios de grises mucho más abruptos, lo que conlleva a una perdida de detalle.
Se puede notar mucho más donde los detalles de la imagen original suelen ser más suaves.

Veamos ahora 2 imágenes, a la izquierda la muestra a 6 bits, y a la derecha la muestra a 4 bits

La imagen original respecto a 6 bits parece que mantiene muy bien su detalle, y respecto a 4 sigue manteniéndose mucho detalle, pero ya podemos empezar a observar ciertos cambios no tan sutiles en ciertas regiones de la imagen que tenían un color muy parecido, al fin y al cabo con 4 bits tenemos 16 tonos de gris.

Pasemos a ver 2 bits, es decir solo 4 tonos de gris

Sí, definitivamente ahora se nota mucho, recordemos que solo tenemos 4 tonos de gris por píxel, podríamos pensar que la imagen se vería muchísimo peor, pero no.
Con solo 4 tonos de gris seguimos manteniendo cierto detalle de las montañas, los árboles…

Ahora pasemos al gran final, 1 único bit, es decir 2 tonos de gris, o luminosidad mínima o máxima

Ya está, ahora solo es una silueta, 2 únicas posibilidades para cada píxel, ya que cada píxel no puede tener un gris intermedio, ya que lo estamos cuantificando a 1 bit, aproximando a 2 únicos valores, no hay continuidad.

Aquí os dejo otro ejemplo, en este caso con 8, 3, 2 y 1 bit.